Подобные треугольники: определение, признаки и свойства
. Объясняют учителя математики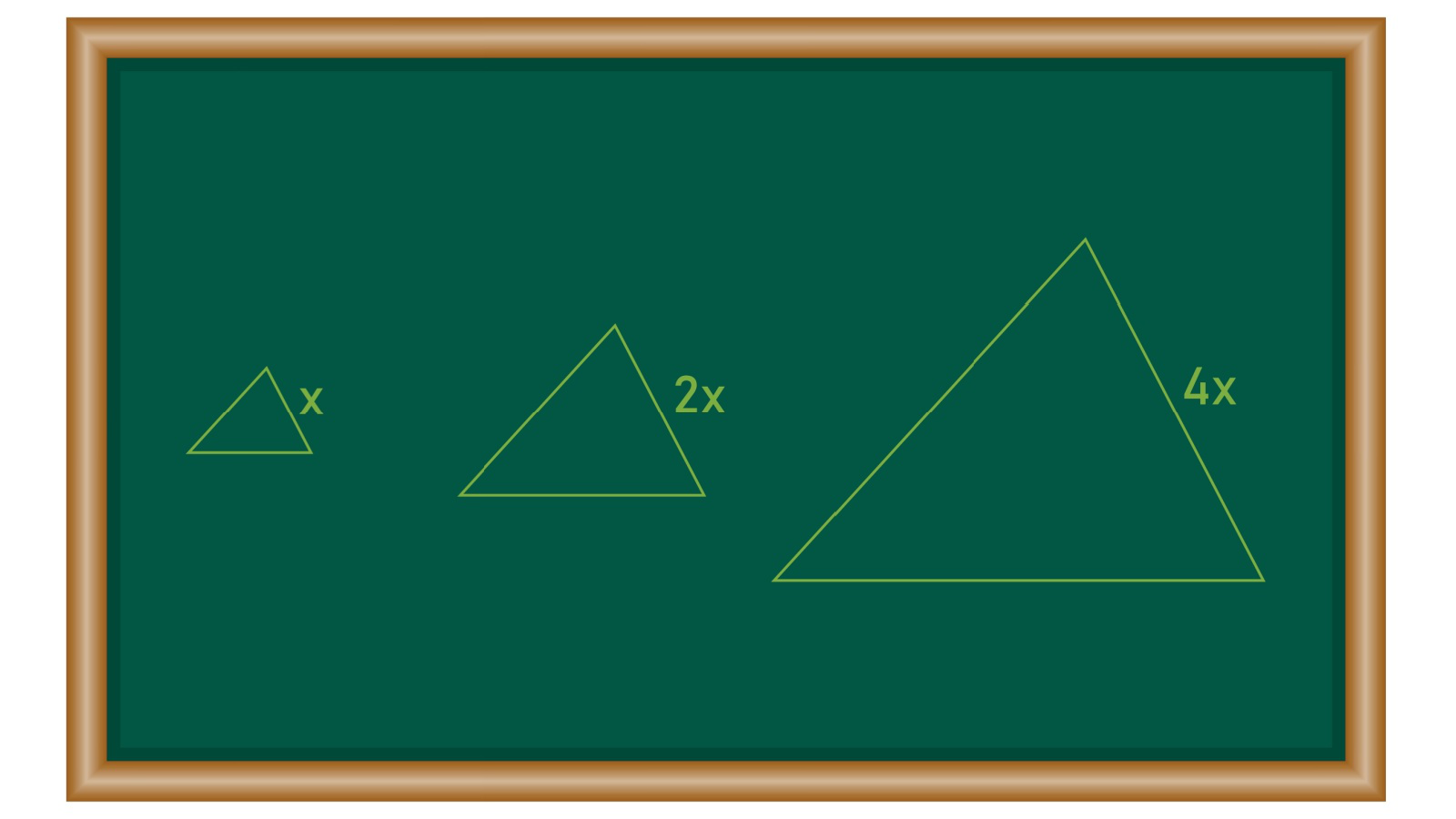
Подобные треугольники — одна из важных тем в геометрии, которая помогает понять, как фигуры могут сохранять форму при изменении размеров. РБК Life вместе с учителями математики объясняет, почему треугольники называют подобными и как определить подобие треугольников.
Что такое подобные треугольники
Подобные треугольники — это геометрические фигуры, которые выглядят одинаково, но их размеры пропорционально отличаются. Например, если треугольники АВС и А1В1С1 имеют одинаковые углы, а все стороны треугольника АВС в два раза больше соответствующих сторон А1В1С1, то такие треугольники считаются подобными [1].
Для обозначения подобия используется символ ∼. Если два треугольника подобны, то мы записываем выражение как △АВС ∼ △А1В1С1. Коэффициент подобия обозначают k. Он показывает, во сколько раз стороны одного треугольника больше или меньше сторон другого треугольника.
Подобные треугольники АВС и А1В1С1
Подобие в математике — такое отношение между фигурами, когда они имеют одинаковую форму, но могут быть разного размера. Представьте, что у вас есть фотография. Если вы увеличите ее или уменьшите, человек на фото будет выглядеть так же — с теми же пропорциями, только крупнее или мельче.

Признаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны [2].
Первый признак подобия треугольников
Признак работает, потому что в треугольнике сумма углов всегда равна 180°. Если у двух треугольников совпадают два угла, то совпадает и третий. Раз все углы равны, значит, треугольники имеют одинаковую форму даже при разных размерах. Например, если взять два треугольника, в каждом из которых есть углы 30° и 90°, то такие треугольники будут подобны, даже если один из них в два раза больше другого.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и угол между этими сторонами совпадает, то треугольники подобны.
Например, у треугольника ABC стороны AB = 6, AC = 8, угол A = 90°, а у треугольника A₁B₁C₁ стороны A₁B₁ = 3, A₁C₁ = 4, угол A₁ = 90°. Проверим пропорцию сторон: AB / A₁B₁ = 6 / 3 = 2, AC / A₁C₁ = 8 / 4 = 2. Стороны пропорциональны (коэффициент = 2), угол между ними одинаков, значит: треугольники подобны, △АВС ∼ △А1В1С1
Второй признак подобия треугольников
Такие треугольники имеют совершенно одинаковую форму — ведь угол зафиксирован, а стороны «масштабированы» в одном и том же отношении. Значит, третий угол и третья сторона автоматически получаются в том же отношении.
Третий признак подобия треугольников
Если все три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны.
Третий признак подобия треугольников
По теореме косинусов или через построение треугольника его углы полностью определяются его сторонами. Если стороны заданы в одинаковой пропорции, то и углы автоматически получаются одинаковыми.
Свойства подобных треугольников
Отношение периметров подобных треугольников
Периметр — сумма всех сторон фигуры. Если два треугольника подобны, то все их соответствующие стороны относятся в одном и том же отношении, равном коэффициенту подобия k. Следовательно, отношение периметров подобных треугольников также равно коэффициенту подобия: k = P1 / P2 [3].
Например, если коэффициент подобия k = 2, а периметр меньшего треугольника P2 = 12 см, то периметр большего треугольника P1 можно найти по формуле: P1 = k × P2 = 2 × 12 = 24 см.
Отношение площадей подобных треугольников
Для подобных треугольников отношение площадей равно квадрату коэффициента подобия: k2 = S1 / S2 [4].
Площадь треугольника S вычисляется как половина произведения основания b, умноженная на высоту h: S = 1 / 2 × b × h. В подобных треугольниках все соответствующие линейные размеры (стороны, высоты, медианы) относятся друг к другу как коэффициент подобия k. Когда мы вычисляем площадь одного подобного треугольника, мы умножаем два линейных размера — основание и высоту, поэтому коэффициент подобия возводится в квадрат.
Отношение длин соответствующих элементов подобных треугольников
Если стороны одного подобного треугольника больше в k раз, то и все остальные элементы тоже будут больше в k раз. Так происходит, потому что все элементы подобных треугольников (стороны, высоты, медианы, биссектрисы) пропорциональны с коэффициентом подобия.
Задачи про подобные треугольники
Задача 1
Условие: В треугольниках ABC и А1В1С1 известно, что они подобны. Коэффициент подобия k = 3. Если сторона большего треугольника AB = 6 см, найдите длину соответствующей стороны А1В1.
Решение: Коэффициент подобия показывает, во сколько раз стороны одного треугольника больше или меньше соответствующих сторон другого. Длина стороны в меньшем треугольнике равна длине стороны в большем треугольнике, поделенной на коэффициент подобия. А1В1 = AB / k = 6 / 3 = 2 см.
Ответ: А1В1 = 2 см.
Задача 2
Условие: Два треугольника ABC и А1В1С1 подобны, коэффициент подобия k = 4. Периметр меньшего треугольника P1 = 15 см. Найдите периметр большего треугольника P.
Решение: Периметр подобных треугольников пропорционален коэффициенту подобия. Следовательно, P = k × P1 = 4 × 15 = 60 см.
Ответ: P = 60 см.
Задача 3
Условие: Два треугольника ABC и А1В1С1 подобны, коэффициент подобия k = 3. Площадь меньшего треугольника S1 = 12 см². Найдите площадь большего треугольника S2.
Решение: Площадь подобных треугольников пропорциональна квадрату коэффициента подобия, следовательно: S2 = k2 × S1 = 32 × 12 = 9 × 12 = 108 см².
Ответ: S2 = 108 см².
Частые вопросы
Как используют подобные треугольники в жизни?
Подобные треугольники помогают нам сохранять правильные пропорции, работать с моделями и измерять объекты косвенным способом — это удобно и реально используется в повседневной жизни. Например, когда архитекторы строят модели зданий в уменьшенном масштабе, с помощью подобных треугольников они могут проверить пропорции перед реальным строительством.

Чем отличаются равные и подобные треугольники?
Равные треугольники полностью совпадают по форме и размеру: у них равны все стороны и все углы. Если один треугольник наложить на другой, они совпадут полностью. Подобные треугольники имеют одинаковую форму, но их размеры могут отличаться: углы равны, а стороны находятся в одинаковом отношении, то есть пропорциональны. Один треугольник можно получить из другого с помощью увеличения или уменьшения.

Как получить подобные треугольники?
Если внутри треугольника провести линию, параллельную одной из его сторон, и эта линия пересекает другие две стороны треугольника, то образуется новый, меньший треугольник, который подобен исходному.

Главное про подобные треугольники
- Подобные треугольники имеют одинаковую форму, но различаются размерами; соответствующие стороны пропорциональны, а углы равны.
- Символ ∼ используют для записи подобия, коэффициент подобия k показывает отношение размеров треугольников.
- Два треугольника подобны, если два угла одного равны двум углам другого.
- Две стороны одного треугольника пропорциональны двум сторонам другого, и угол между ними совпадает.
- Все три стороны одного треугольника пропорциональны трем сторонам другого.
- Отношение периметров подобных треугольников равно коэффициенту подобия k.
- Отношение площадей равно квадрату коэффициента подобия.
- Все элементы треугольников (стороны, высоты, медианы, биссектрисы) пропорциональны коэффициенту подобия.
- Равные треугольники совпадают полностью по форме и размеру, а подобные — только по форме.
- Проведение линии, параллельной одной из сторон, внутри треугольника создает новый, подобный исходному.