Что такое медиана треугольника
. Формулы, свойства и способы нахождения медианы
Медиана треугольника — это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны
Медиана треугольника может встретиться во всех заданиях по геометрии на ЕГЭ по профильной математике. На ЕГЭ по базовой математике свойства медианы могут пригодиться в заданиях 12 и 13. РБК Life вместе с экспертами рассказывает, как запомнить формулы медианы и применять их на практике.
Что такое медиана треугольника
Медиана треугольника — это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны. У любого треугольника три медианы. В геометрии медиану обычно обозначают как mn, где n — сторона, к которой идет медиана.
Название этого отрезка произошло от латинского слова mediāna, которое переводится как «средняя» [1].
Красным цветом обозначены медианы треугольника
[Есть] стишок для запоминания определения медианы:
«Медиана — обезьяна,
У которой зоркий глаз.
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас».

Формула медианы треугольника
Длину медианы можно найти по двум формулам:
- mb= ½√ (a2+c2+2ac*cosB), где a, b, c — стороны треугольника, B — угол между сторонами a и с;
- ma= ½*√ (2b2+2c2−a2), где a, b, c — стороны треугольника [2].
Свойства медианы треугольника
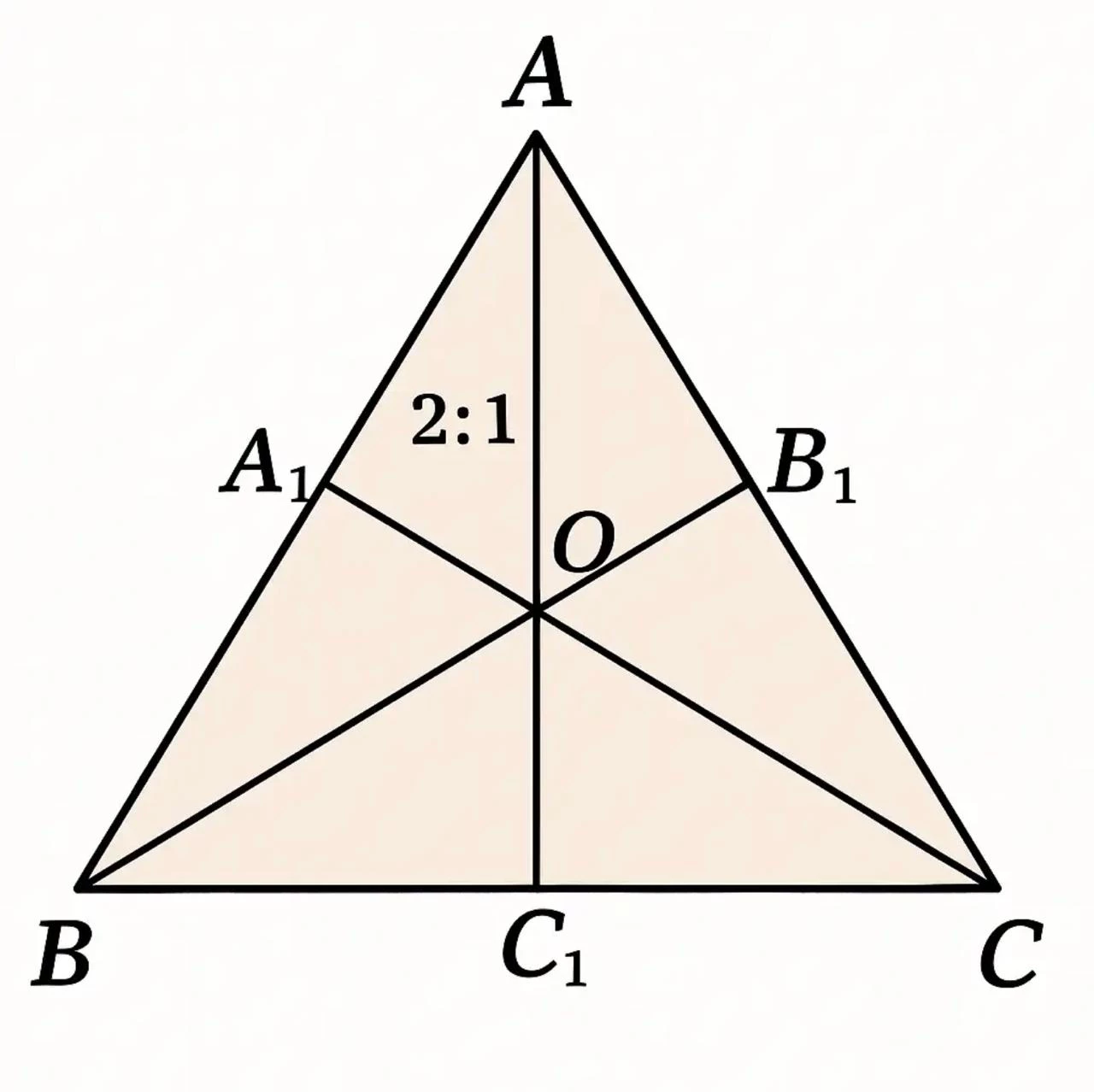
- Медианы пересекаются в одной точке и делятся этой точкой в отношении 2:1 от вершины.
- Медиана разбивает треугольник на два равновеликих по площади треугольника. Площадь треугольника ABB1 равна площади треугольника CBB1 и равна ½ площади треугольника ABC.
- Медианы треугольника делят его на шесть равновеликих треугольников. Площади треугольников AOB1, COB1, COA1, BOA1, BOC1, AOC1 равны.
- Если О — точка пересечения медиан треугольника ABC, то площадь треугольника AOC равна площади треугольника BOC и равна ⅓ площади ABC.
Методист по математике «Онлайн-школы № 1» Мария Пудлич рассказала РБК Life, что первое свойство часто применяется в заданиях ОГЭ и первой части ЕГЭ. Свойства 2–4 встречаются в сложных заданиях на ЕГЭ.
Треугольник ABC. В центре — точка пересечения медиан
Длину стороны, а треугольника по трем известным медианам вычисляют по специальной формуле (представлена на картинке ниже). Это свойство рассматривают в классах с углубленным изучением математики.
Формула для вычисления стороны треугольника по трем известным медианам
Медиана в разных типах треугольников
Медиана в равностороннем треугольнике
- Все медианы в равностороннем треугольнике равны.
- Любая медиана в равностороннем треугольнике является также биссектрисой и высотой.
Медиана в прямоугольном треугольнике
- Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине этой гипотенузы.
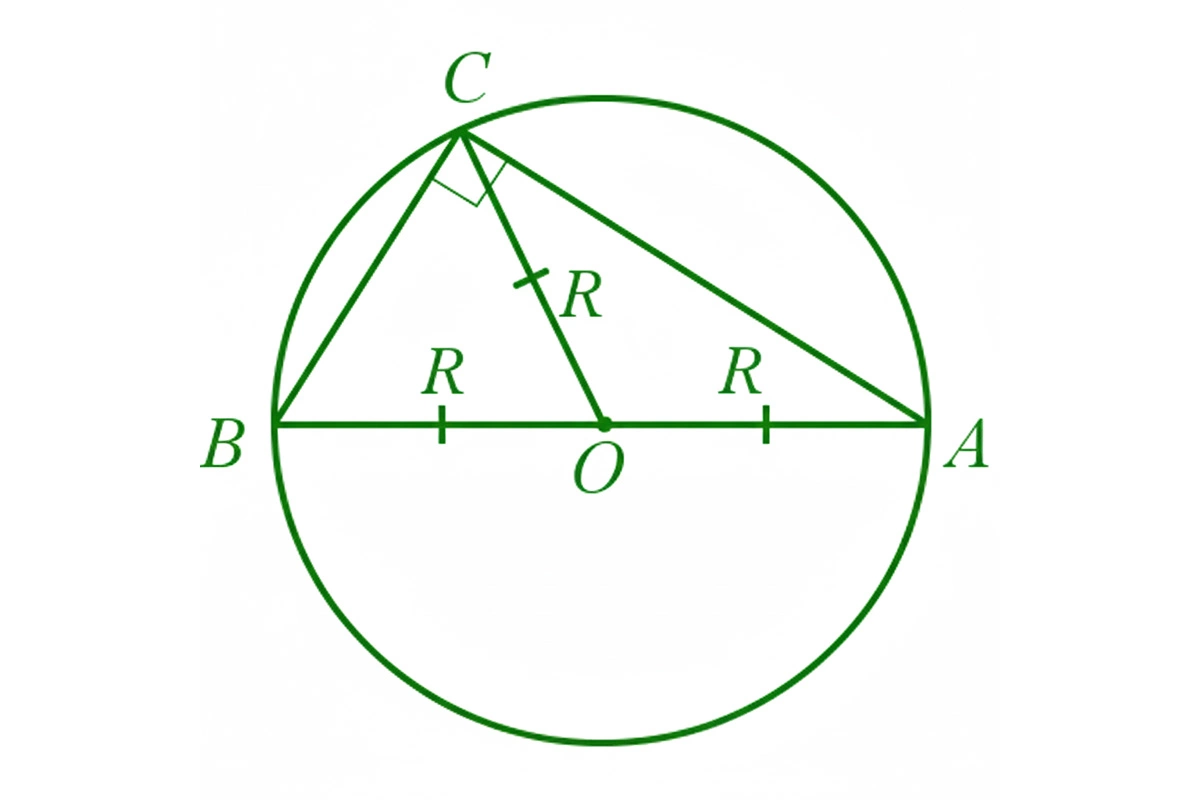
- Медиана в прямоугольном треугольнике равна радиусу окружности, описанной около этого треугольника.
Медиана в прямоугольном треугольнике равна радиусу окружности, описанной около этого треугольника
Медиана в равнобедренном треугольнике
Медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой. Биссектриса — это луч, исходящий из вершины угла и делящий угол пополам. Высота — перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону.
Как же запомнить все определения и свойства [медианы]?
- Визуализация. Сделайте рисунки по каждому свойству и поймите, как оно устроено. Осознав суть с точки зрения геометрии, вы сможете легко воспроизвести свойства и с использованием других обозначений.
- Практика. Решите несколько однотипных задач, где нужно найти длину медианы или применить ее свойство. Повторение — мать учения.
- Мнемонические приемы. Например, для запоминания свойства, что медиана из вершины прямого угла равна половине гипотенузы, можно представить прямоугольник и мысленно провести его диагонали. Помним, что диагонали прямоугольника точкой пересечения делятся пополам и они равны. А половина одной из диагоналей и есть медиана прямоугольного треугольника, у которого гипотенуза — другая диагональ.

Школьная планиметрия в целом очень объемна. Многие свойства [ученики] проходят, но не так часто отрабатывают, поэтому их легко забыть. Нужно научиться понимать геометрию, видеть взаимосвязи между темами. В таком случае не придется ничего зубрить. Большую часть необходимой информации можно будет выводить прямо на экзамене. Для этого «пройдитесь» по всей теории с самого нуля и закройте пробелы. После — важно много практиковаться, чтобы точно закрепить весь изученный или повторенный материал.

Задачи на медиану треугольника
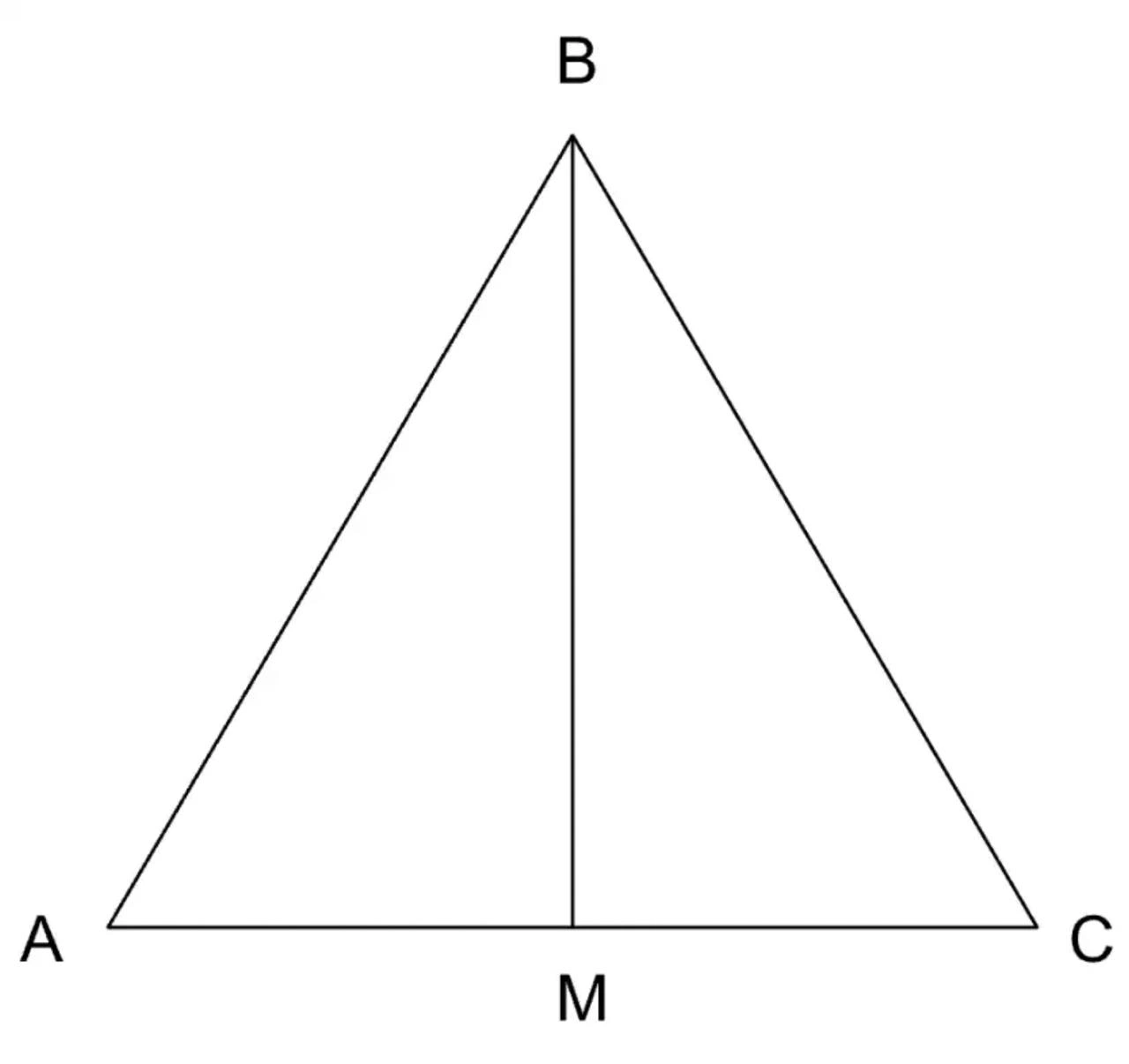
Задача № 1. В треугольнике ABC провели медиану BM. Найдите площадь треугольника BCM, если площадь треугольника ABC равна 20 см.
Иллюстрация к задаче № 1
Решение. Медиана треугольника делит его на два равновеликих, то есть равных по площади треугольника. Площадь каждого из них будет составлять половину от площади исходного. Чтобы найти площадь треугольника BCM, нужно поделить площадь треугольника ABC на 2. 20: 2 = 10. Ответ: площадь треугольника BCM равна 10 см.
Задача № 2. Из вершины C треугольника ABC проведена медиана CM. Найдите сторону AB треугольника ABC, если она в 2 раза больше CM. AC = 24 см, BC = 7 см.
Решение. Так как сторона AB в 2 раза больше медианы, проведенной к ней, то это прямоугольный треугольник и AB в нем — гипотенуза. По теореме Пифагора: AB2 = AC2 + BC2. Получается, AB2=242 + 72=576 + 49 = 625. Получается, AB = √AB2 = √625 = 25. Ответ: сторона AB равна 25 см.
Задача № 3. Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN = 33 см, CM = 15 см. Найдите AO.
Решение. Так как M и N — середины сторон треугольника, то AN и CM — медианы треугольника. По свойству медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2:1 от вершины. Исходя из этого, AO = ⅔*AN = 22. Ответ: отрезок AO равен 22 см.